Student-t hypotesetest av gjennomsnitt

Hvis vi skal gjøre hypotesetester på gjennomsnittet til et utvalg så støter vi fort på problemer hvis utvalget vårt $n$ er lite. Det er da mindre sannsynlig at utvalget vårt er normalfordelt (se Sentralgrenseteoremet), og det er veldig vanskelig å bestemme $\sigma$.

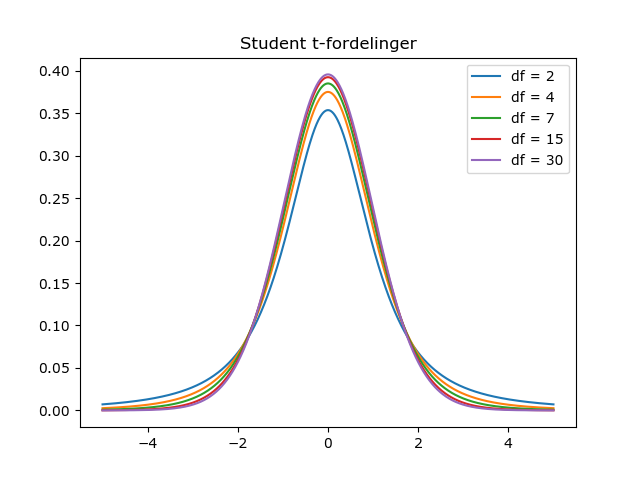
Istedenfor å bruke normalfordeling bruker vi derfor en annen fordeling: student-t fordelingen. Den ligner på normalfordelingen, men vi er her nødt til å ta hensyn til antall frihetsgrader $\nu =n-1$.^[1] når $\nu \to \mathrm{\infty }$ så vil t-fordelingen bli lik normalfordelingen.

For å gjennomføre en hypotesetest forventningsverdien til $X$ så må man:

1. Sette opp nullhypotese og alternativ hypotese
2. Samle inn observasjoner
3. Finne gjennomsnittet til observasjonene
4. Finne variansen, $s^2$ til observasjonene ved å summere kvadratavvikene og dividere på antallet observasjoner $s^2=\frac{\sum (x_i-\overline{x}{)}^2}{n-1}$.
5. Beregne standardavviket $s$
6. Beregne $t$-verdien: $t=\frac{\overline{x}-{\mu }_0}{\frac{s}{\sqrt{n}}}$
7. Bruke statistisk programvare til å beregne $P(T\le t)$

# venstresidig test. H_a: mu er mindre enn mu_0
from scipy.stats import t
import numpy as np
mu_0 = 15
obs = [220, 205, 209, 256, 214]
df = len(obs)               # antall frihetsgrader = n - 1
x_strek = np.average(obs)   # beregne gjennomsnitt
SF = np.std(obs, ddof=1)    # beregne standardavvik 
							# med n-1 frihetsgrader
t_obs = (x_strek - mu_0) / SF
P = t.cdf(t_obs, df)        # bruker den kumulative sannsyn-
							# lighetsfordelingen til å bestemme
							# for observasjonene våre kan skje
							# gitt at H_0 er sann

# for å visualisere testobservator fra forrige test
import matplotlib.pyplot as plt
from scipy.stats import t
import numpy as np

x = np.linspace(-5,5,1000)
T = t.pdf(x, df=df)
plt.plot(x,T)
femprosent = t.ppf(0.05, df=df)
nittifemprosent = t.ppf(0.95, df=df)
plt.vlines(femprosent,0,max(T), color="red", label="95% persentil")
plt.vlines(femprosent,0,max(T), color="red", label="95% persentil")
plt.vlines(t_obs,0,max(T), color="magenta", label="t_observator")
plt.legend()